The centroid is the term for 2-dimensional shapes. BarY frac4R3π Example.
Chapter 5 Centroids And Centers Of Gravity 1
2
Centroids Of Plane Areas
A25m b15m and and c2.
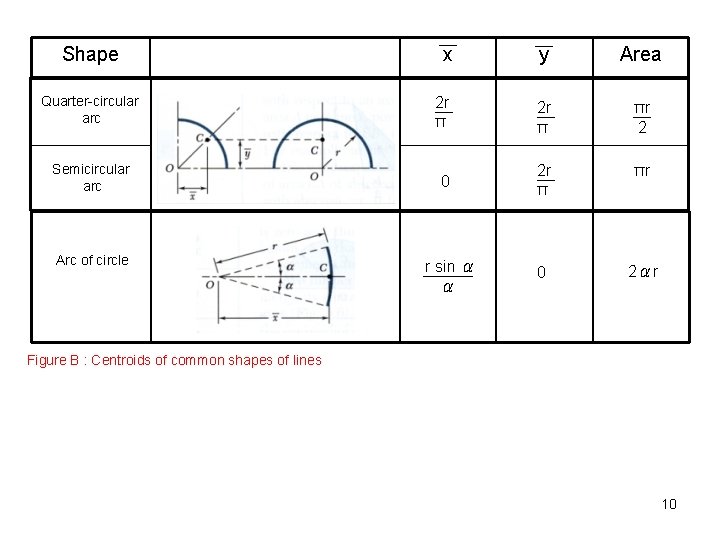
Centroid of semicircle. Areas to bending stress and deflection. 1Area Integral from. Jo is the polar moment of inertia about some noncontroidal point Jc is the polar moment of inertia about the centroid and dis the distance between the points and T X1 11 yi x Figure 2 As shown a rectangle has a base of b 5 80 ft and a height of h 120 ft Figure 2 The rectangles bottom is located at a distance yı 210 ft from the xaxis and the rectangles left edge is located.
Let R be a circle of radius 1 centered at Use the theorem of Pappus for volume to find the volume of the torus generated by revolving R around the -axis. To find the centroid you find the average of the x and y values of. The second moment of area also known as area moment of inertia is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axisThe unit of dimension of the second moment of area is length to fourth power L 4 and should not be confused with the mass moment of inertia.
A sphere is a body of revolution formed by the rotation of a semicircle with the diameter of the semicircle as its axis of rotation. Divide the area into a triangle rectangle and semicircle with a circular cutout. 716 Semicircular Arc and Lines Centroid of Composite Figure.
The centroid of cross-sectional areas of beams Figure 61 Relative resistance of four beam and columns will be used later as the reference origin for cross-sections with the same cross-sectional computing other section properties. The centroid travels around the -axis in a circular path of radius 4 so the centroid travels units. If so then the area would be.
11 21 Moment of Inertia - Composite Area Monday November 26 2012 Using the Table. Using a single integral we were able to compute the center of mass for a one-dimensional object with variable density and a two dimensional object with constant density. Circular segments are implemented in the Wolfram Language as DiskSegmentx y r q1 q2.
Round off only on the final answer expressed in 3 decimal places. The volume of the ball is calculated as follows. Eureka Math Grade 6 Module 1 Ratios and Unit Rates Eureka Math Grade 6 Module 1 Topic A Representing and Reasoning About Ratios.
709 Centroid of the area bounded by one arc of sine curve and the x-axis. This point is an equal distance from each corner vertex of the triangle. Find the centroid of semi-circle whose radius is 10cm and of 20cm diameter.
Ix π8. The point in which the three medians of the triangle intersect is known as the centroid of a triangle. ----- Is this basically 14 of an ovalellipse.
Find the centroid of the shaded area as shown in fig Find the centroid of the shaded area as shown in fig. It is the point that matches to the center of gravity of a particular shape. A portion of a disk whose upper boundary is a circular arc and whose lower boundary is a chord making a central angle radians illustrated above as the shaded regionThe entire wedge-shaped area is known as a circular sector.
Get to know about the step-by-step process of adding integers rules to add two integers and solved examples in the following sections. EngageNY Math Grade 6 Module 1 Answer Key Eureka Math 6th Grade Module 1 Answer Key. 708 Centroid and area of spandrel by integration.
Integers are numbers that do not have fractions or decimals. Inertia about the base of the semicircle not the centroid y x 10 212 5 6in 8 in. Find the centroid of the shaded area as shown in fig.
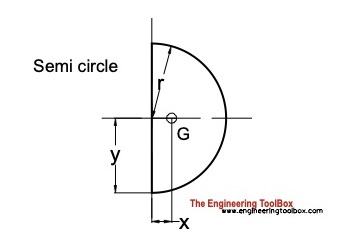
Then the volume of the torus is units 3. Centroid of semicircle using integration formulas. The centroid of a triangle is its center-most point.
It is the point which corresponds to the mean position of all the points in a figure. The centroid is the centre point of the object. Subtract the area and first moment of the circular cutout.
715 Semicircle and Triangle Centroid of Composite Figure. The given below is the online critical number calculator for you to calculate the same. The particles discussed in this paper are all spherical.
714 Inverted T-section Centroid of Composite Figure. Find the centroid of the shaded area as shown in fig. Find the area of the parallelogram determined by the vectors v and w where v2i3k and w2j-3k.
The centroid is an important property of a triangle. To move it to the moment of inertia about the x-axis we have to make two steps 2 base to centroid 2. 706 Centroid of quarter circle by integration.
Find the exact coordinates of the centroid. 715 Semicircle and Triangle Centroid of Composite Figure. The coordinate system to locate the centroid with can be anything we want.
A centroid is the central point of a figure and is also called the geometric center. Determine the x-component m of the centroid of the given figure if the cut portion is a semicircle of radius 6m and other dimensions are. Iy height width³ - height a width² width height a² 36 where a is a top vertex displacement.
Centroid usually refers to the centers of lines areas and volumes. Half circle is known as semi-circle. Just enter the expression to find the critical numbers of the function with ease.
Let us discuss the definition of centroid formula properties and centroid for different geometric shapes in detail. Derive the formulas for the location of semicircle centroid. Ix width height³ 36.
714 Inverted T-section Centroid of Composite Figure. In other words if both the x-axis and the y-axis cross the centroid of the analyzed shape then these equations hold. Centroid of semi-circle is at a distance of 4R3π from the base of semi-circle.
Centroid of Semi-circle Formula. The following is a list of second moments of area of some shapes. 707 Centroid of quarter ellipse by integration.
Analytical formulas for the moments of inertia second moments of area I x I y and the products of inertia I xy for several common shapes are referenced in this pageThe considered axes of rotation are the Cartesian xy with origin at shape centroid and in many cases at other characteristic points of the shape as well. As shown in the figure below. Find the centroid of the shaded area as shown in fig.
Find the total area and first moments of the triangle rectangle and semicircle. 709 Centroid of the area bounded by one arc of sine curve and the x-axis. 3 V 1 4 3 π R 3.
So the X coordinate would equal. Find the centroid of the shaded area as shown in fig. Where V 1 is the volume of the sphere R is the radius of the sphere.
A b2 b2 с Add your answer Question 2 10 Points Determine the y-component mm of the centroid of the plane figure. 717 Symmetrical Arcs and a Line. One can perform fundamental arithmetic operations on two or more integers.
Y sqrtx y 0 x 9. Compute the coordinates of the area centroid by dividing the first moments by the total area.
2

Mechanical Engineering Centroids Center Of Gravity 6 Of 35 Center Of Gravity Of A Semi Circle Youtube
Centroid Of A Semicircle Physics Forums

Prove By Integration That The Coordinates Of Centroid Of This Semi Circle Is R 2r Pi Study Com
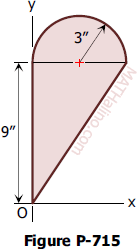
715 Semicircle And Triangle Centroid Of Composite Figure Engineering Mechanics Review At Mathalino
2

Quiz Worksheet Semicircle Centroid Center Of Mass Study Com

The Centroid Positions Of The Semi Circle A Rectangle B And Download Scientific Diagram